Quinze questões discursivas

Resolver questões discursivas requer atenção e domínio sobre os assuntos envolvidos em cada questão, de forma geral questões discursivas tratam de mais de um conteúdo.

Confira a seguir 15 questões discursivas envolvendo diversos tópicos de matemática, as resoluções no final do artigo.
Use os comentários para solucionar suas dúvidas.
1) Considere o teorema e os dados a seguir para a resolução desta questão.
Se α, β e α + β são três ângulos diferentes de 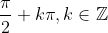 , então
, então =\frac{tg\alpha&space;\pm&space;tg\beta&space;}{1\mp&space;tg\alpha&space;.tg\beta&space;}) . E a, b e c são três ângulos agudos , sendo tb = 2 e tg (a + b + c) = 4/5.
. E a, b e c são três ângulos agudos , sendo tb = 2 e tg (a + b + c) = 4/5.
Calcule tg (a - b + c).
2) Um tabuleiro retangular com pregos dispostos em linhas e colunas igualmente espaçadas foi usado em uma aula sobre área de polígonos. A figura abaixo representa o tabuleiro com um elástico fixado em quatro pregos indicados pelos pontos A, B, C e D.

Considere u a unidade de área equivalente ao menor quadrado que pode ser construído com vértices em quatro pregos do tabuleiro. Calcule, em u, a área do quadrilátero ABCD formado pelo elástico.
3) Moedas idênticas de 10 centavos de real foram arrumadas sobre uma mesa, obedecendo à disposição apresentada no desenho: uma moeda no centro e as demais formando camadas tangentes. Considerando que a última camada é composta por 84 moedas, calcule a quantia, em reais, do total de moedas usadas nessa arrumação.

4)Considere um setor circular AOC, cujo ângulo central θ é medido em radianos. A reta que tangencia o círculo no extremo P do diâmetro CP encontra o prolongamento do diâmetro AB em um ponto Q, como ilustra a figura.

Sabendo que o ângulo θ satisfaz a igualdade tg θ = 2θ, calcule a razão entre a área do setor AOC e a área do triângulo OPQ.
5) Um cilindro circular reto é inscrito em um cone, de modo que os eixos desses dois sólidos sejam colineares, conforme representado na ilustração abaixo. A altura do cone e o diâmetro da sua base medem, cada um, 12 cm. Admita que as medidas, em centímetros, da altura e do raio do cilindro variem no intervalo ]0;12[ de modo que ele permaneça inscrito nesse cone.

Calcule a medida que a altura do cilindro deve ter para que sua área lateral seja máxima.
6) O preço dos produtos agrícolas oscila de acordo com a safra de cada um: mais baixo no período da colheita, mais alto na entressafra. Suponha que o preço aproximado P, em reais, do quilograma de tomates seja dado pela função ![P(t)=0,8.sen[\frac{2\pi}{360}.(t-101)]+2,7](http://latex.codecogs.com/gif.latex?P(t)=0,8.sen[\frac{2\pi}{360}.(t-101)]+2,7) , na qual t é o número de dias contados de 1° de janeiro até 31 de dezembro de um determinado ano.
, na qual t é o número de dias contados de 1° de janeiro até 31 de dezembro de um determinado ano.
Para esse período de tempo, calcule:
a) o maior e o menor preço do quilograma de tomates;
b) os valores t para os quais o preço seja igual a R$ 3,10.
7) Em uma barraca de frutas, as laranjas são arrumadas em camadas retangulares, obedecendo à seguinte disposição: uma camada de duas laranjas encaixa-se sobre outra camada de seis; essa camada de seis encaixa-se sobre outra de doze; e assim por diante, conforme a ilustração abaixo.

Sabe-se que a soma dos elementos de uma coluna do triângulo de Pascal pode ser calculada pela fórmula 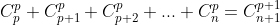 , na qual n e p são números naturais, n ≥ p e
, na qual n e p são números naturais, n ≥ p e 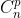
corresponde ao número de combinações simples de n elementos tomados p a p.
Com base nessas informações, calcule:
a) a soma 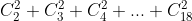 .
.
b) o número total de laranjas que compõem quinze camadas.
8) Uma caixa d’água tem o formato de um tronco de pirâmide de bases quadradas e paralelas, como mostra a figura abaixo, na qual são apresentadas as medidas referentes ao interior da caixa.

a) Qual o volume total da caixa d’água?
b) Se a caixa contém (13/6) m3 de água, a que altura de sua base está o nível d’água?
9) Suponha que um livro de 20 cm de largura esteja aberto conforme a figura abaixo, sendo DAC = 120° e DBC = 60°.

a) Calcule a altura AB do livro.
b) Calcule o volume do tetraedro de vértices A, B, C e D.
10) Dois prêmios iguais serão sorteados entre dez pessoas, sendo sete mulheres e três homens. Admitindo que uma pessoa não possa ganhar os dois prêmios, responda às perguntas abaixo.
a) De quantas maneiras diferentes os prêmios podem ser distribuídos entre as dez pessoas?
b) Qual é a probabilidade de que dois homens sejam premiados?
c) Qual é a probabilidade de que ao menos uma mulher receba um prêmio?
11) Um estudante tinha de calcular a área do triângulo ABC , mas um pedaço da folha do caderno rasgou-se.

Ele, então, traçou o segmento A'C' paralelo a AC , a altura C'H do triângulo A'BC' e, com uma régua, obteve estas medidas:
C'H = 1,2cm, A'B = 1,4cm e AB = 4,2cm .
a) Use essas medidas e calcule a área do triângulo ABC .
b)Com a régua, ele mediu também o lado A'C' e obteve A´C´=1,5cm.
Se as medidas em graus dos ângulos agudos A e B são respectivamente a e b , calcule o valor de sen(a - b).
12) Um meteorito foi detectado por astrônomos nas proximidades da Terra e cálculos feitos mostraram que ele deveria atingir a superfície em uma região deserta, com a forma de um retângulo ABCD. Sabe-se que a área da região S, que tem a forma de um trapézio retângulo, mede 7km2.

Expresse, em porcentagem, a probabilidade de o meteorito cair na região R ou na região T.
13)
a) Determine o comprimento do lado de um quadrado, sabendo que um de seus lados está contido no lado AB de um triângulo eqüilátero ABC , e os outros dois vértices pertencem aos lados AC e BC . Dados: A(0,0),B(36,0) , e o terceiro vértice, C , está no 1º quadrante. Considere as medidas dos lados do triângulo expressas em metros.
b) Um engenheiro pretende construir uma piscina em seu sítio, dentro de um terreno que tem a forma de um triângulo eqüilátero e a mesma área do triângulo do item A desta mesma questão. A piscina deve ter cerca de 1,5 m de profundidade, deve ocupar a maior área possível, e a borda deve ter a forma de uma circunferência.
De quantos litros de água, aproximadamente, ele vai necessitar, para encher completamente a piscina?
Se necessário, utilize o valor 3,14 para π .
14) O conhecimento que temos da matemática na Antigüidade vem, em boa parte, de textos matemáticos redigidos por escribas, propondo problemas para os alunos ou outros escribas resolverem. Leia com atenção esta adaptação do texto “Sou o escriba, o chefe dos trabalhadores”, e resolva o problema que o autor propõe como um desafio a outro escriba:
Temos de resolver um problema e calcular certa taxa de juro. Um velho mercador emprestou um capital de 8 moedas de ouro, a certa taxa anual de juro composto, durante três anos. Passado esse tempo, o velho mercador ficou muito contente: somente de juros, ele recebeu 19 moedas de ouro!
Os escribas estarão todos reunidos para descobrir a taxa de juro da aplicação, mas nenhum saberá como fazê-lo. Voltar-se-ão para ti e te dirão: “Tu és um escriba hábil, meu amigo! Responde rápido para nós, honra tua reputação, para que não se possa dizer que existe alguma coisa que o chefe dos escribas não saiba: a que taxa anual de juro composto o mercador aplicou o seu dinheiro?”
15) Um programa de TV tem um quadro em que o apresentador exibe uma caixa fechada que contém um cheque preenchido. Ganhará a quantia equivalente, em dinheiro, o espectador que, por telefone, com um único palpite, adivinhar o valor do cheque. Decorridos quinze minutos, não havendo vencedor, o apresentador fornecerá as seguintes informações sobre o valor do cheque, em reais: é um número inteiro, composto por algarismos distintos, par, não divisível por 10, maior que 30 mil e menor que 50 mil.
a) Conhecidas essas informações, qual a probabilidade de um espectador ganhar a quantia prometida?
b) Se, ainda assim, não houver vencedor, decorridos mais dez minutos de programa, o apresentador dirá que aceitará duas tentativas e que o valor do cheque é um número terminado em 04. Qual a probabilidade de um espectador acertar o valor do cheque na segunda tentativa?
Comentários
comentários


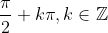 , então
, então =\frac{tg\alpha&space;\pm&space;tg\beta&space;}{1\mp&space;tg\alpha&space;.tg\beta&space;}) . E a, b e c são três ângulos agudos , sendo tb = 2 e tg (a + b + c) = 4/5.
. E a, b e c são três ângulos agudos , sendo tb = 2 e tg (a + b + c) = 4/5.![P(t)=0,8.sen[\frac{2\pi}{360}.(t-101)]+2,7](http://latex.codecogs.com/gif.latex?P(t)=0,8.sen[\frac{2\pi}{360}.(t-101)]+2,7) , na qual t é o número de dias contados de 1° de janeiro até 31 de dezembro de um determinado ano.
, na qual t é o número de dias contados de 1° de janeiro até 31 de dezembro de um determinado ano.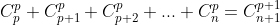 , na qual n e p são números naturais, n ≥ p e
, na qual n e p são números naturais, n ≥ p e 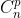
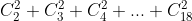 .
.








